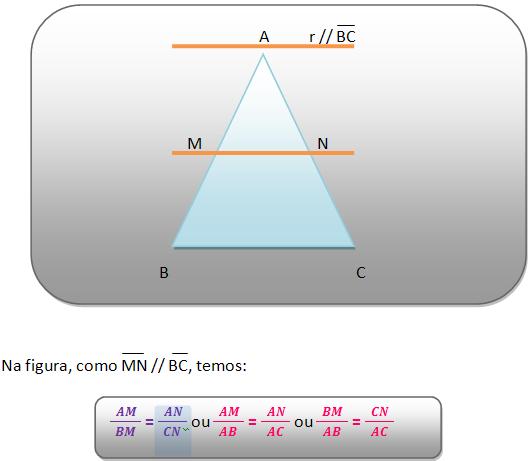
Sempre que houver uma paralela a um lado de um triângulo, que interrompe os outros dois lados, essa paralela irá estabelecer sobre eles pares de segmentos correspondentes e proporcionais.
Vejamos:
COLEGIO: OMEGA, ALUNOS: JOAO FERREIRA E RAFAEL ANDRADE, SERIE 9°ANO B, PROFESSOR LUCIANO REIS.

Pelo Teorema temos que![]()
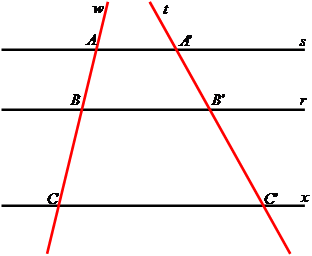
Exemplo 1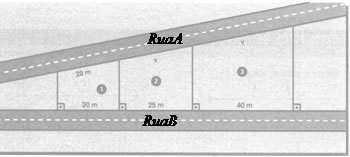
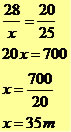
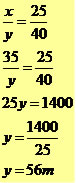
Exemplo 2
Obs.: os fios da rede central são paralelos.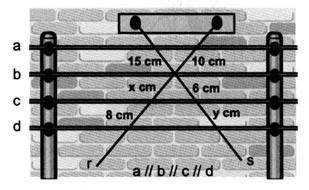
Aplicando o Teorema de Tales, temos: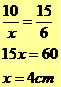
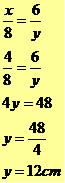
Exemplos resolvidos:
a)  Onde
Onde  , pois senão anularia o denominador
, pois senão anularia o denominador
[Sol] Encontrando o m.m.c dos denominadores: 2x
Então: 
Eliminando os denominadores, pois eles são iguais:
 »
» 
Aplicando a fórmula de Bháskara:


Logo, x = 2 e x` = 4. » S={2,-4}
b ) 
 e
e 
[Sol] m.m.c dos denominadores: (x-1).(x+2)
Então: 
Eliminando os denominadores:
 »
»  »
»  »
» 
* Note que a solução da equação deve ser diferente de 1 e 2 pois senão anularia o denominador, logo a solução da equação será somente:
x=-1 » S={-1}
Equação Irracional é uma equação em que há incógnita em um ou mais radicais. São equações irracionais:

4) ![]()
Resolver a equação:

Se na primeira vez que elevarmos a equação ao quadrado, continuar a existir a raiz quadrada, ela deve ser isolada e a equação será novamente elevada ao quadrado tantas vezes forem necessárias até que não exista mais nenhum radical.
![]()
4º passo: Verificar ,Esta verificação consiste em substituir na equação original os valores de x obtidos.
Observe:

Notamos que 1 é solução da equação mas 6 não é, assim sendo:
S={1}